題目連結
給定一組字串,回傳該組字串中,最長的回文(Palindromic)子字串。例如: 輸入babad ,回傳 bab (或 aba)。
我第一次也只能想到暴力法,作法很簡單,就是把每個子字串拿去判斷是否為回文。同樣以 babad 為例,從 index = 0 開始逐一檢查 b , ba , bab , baba , babad 是否為回文,再來從 index = 1 開始檢查 a, ab , aba , abad ,將每個子字串都跑過一次。
實作程式碼如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public String longestPalindrome ( String s ) {
String longest = "" ;
for ( int i = 0 ; i < s . length (); i ++ ) {
String sub_str = "" ;
for ( int j = i ; j < s . length (); j ++ ) {
sub_str += s . charAt ( j );
if ( isPalindromic ( sub_str ) && sub_str . length () > longest . length ()) {
longest = sub_str ;
}
}
}
return longest ;
}
private boolean isPalindromic ( String s ) {
int start = 0 ;
int end = s . length () - 1 ;
while ( start <= end ) {
if ( s . charAt ( start ) != s . charAt ( end )) {
return false ;
}
start ++ ;
end -- ;
}
return true ;
}
}
而這個解法在 input 字串長度不長的 test case 下是都能成功跑過,但當 input 字串非常長時,就直接 GG 惹。
而我們來看一下他的時間複雜度,外面兩個迴圈在組合所有子字串的過程, 總共跑了 n + (n-1) + (n-2) + … + 1 = n(n-1) / 2 次,就已經達到了 O(n²) 。而每次對該字串檢查是否為回文,同樣需要遍歷每個子字串於是再乘以 n,複雜度來到了 O(n³)。如此高的時間複雜度,會直接 time out 也合理了。
這個版本的解法核心在於:改變我們檢查是否為回文的方法。由於暴力法中檢查回文的方式是傳統的由外而內方式檢查,也就是說,以 bab 為例, 先從頭尾開始檢查是否相同,若是,再將兩邊指標各往中間移動一格,繼續檢查下去。
然而這裡會需要改成由內而外的方式檢查,也就是先認定某個字元為中心點,再往外去檢查左右兩側是否為相同字元。所以可以只需要一層外迴圈遍歷每個字元,在每次的遍歷中,都將當前字元視為回文字串的中心,去往外擴展看能夠達到最長的回文子字串長度。
但這個方法需要另外考慮字串為偶數的情況,例如 cbbd ,其中最長的回文子字串為 bb ,這個情況下要將 bb 視為中心。
實作程式碼如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public String longestPalindrome ( String s ) {
String longest = "" ;
for ( int i = 0 ; i < s . length (); i ++ ) {
// odd
int l = i , r = i ;
while ( l >= 0 && r < s . length () && s . charAt ( l ) == s . charAt ( r )) {
if ( r - l + 1 > longest . length ()) {
longest = s . substring ( l , r + 1 );
}
l -- ;
r ++ ;
}
//even
l = i ;
r = i + 1 ;
while ( l >= 0 && r < s . length () && s . charAt ( l ) == s . charAt ( r )) {
if ( r - l + 1 > longest . length ()) {
longest = s . substring ( l , r + 1 );
}
l -- ;
r ++ ;
}
}
return longest ;
}
}
這個解法可以將複雜度下降到 O(n²):遍歷每個字元 ,每次找尋最大回文子字串再遍歷2次,O(n*2n) 。
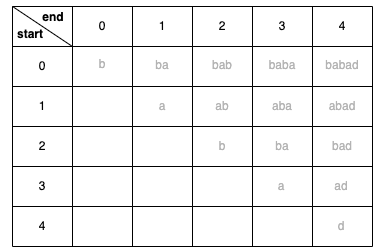
最後來到最難的 DP 解法⋯⋯首先將每個子字串以 (起始位置, 結束位置)的座標來代表,例如:以 babad 為例,(0,2) 代表 起始位置為 index = 0(“b”), 結束位置為 index = 2 (”b”)的子字串 bab 。並且建立一個 row 為起始位置,col 為結束位置的二維陣列,來紀錄該字串是否為回文。
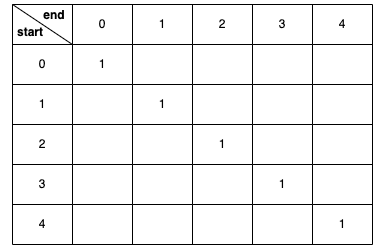
首先來看到 (0,0) 的位置,代表的是起始位置為 0 且結束位置也為 0 的子字串 “b”,而根據回文規則,單一字元視為回文字串,所以在表格上(0,0)裡面可以填 true (代表其為回文字串)。
同理,(1,1)、(2,2)⋯⋯所有長度為 1 的子字串都是回文,於是表格填完會長這樣:
這時候來到 DP 的精髓,也就是如何有效運用前一次的計算結果呢?
假設我們有一組子字串 cabac 座標為(i,j),如果起始位置(i)與結束位置(j)的字元相同,並且中間字串 aba 也是回文的情況下,我們就可以保證,這組子字串也會是回文。
由此可以推導出字串要是回文必須滿足兩個條件:
起始位置的字元需等於結束位置的字元
中間的那組子字串也必須是回文
以座標為(0,2) 的子字串 bab為例:起始位置的字元 b等於結束位置的字元 b。同時查表得知中間的 a 也就是字串(1,1) 是回文,達成條件 1&2 所以該子字串也是回文,並記錄在表上。
而在 (0,3) 的子字串 baba 情況下,起始位置字元 b 與結束位置字元 a 不同,直接不符合回文,也無需再檢查條件 2。
所以我們可以歸納出一個公式:
// pseudo code
substring(i, j) = string[i] == string[j] && substring(i+1, j-1)
實作程式碼如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public String longestPalindrome ( String s ) {
String longest = "" ;
int max = 0 , len = s . length ();
boolean [][] dp = new boolean [ len ][ len ] ;
for ( int l = 0 ; l < len ; l ++ ) {
int start = 0 , end = start + l ;
/**
為了確保每次在查表時,一定可以取得比當前子字串長度還要短的子字串是否為回文的紀錄,
每次會遍歷相同長度的子字串
第一次: b, a, b, a, d
第二次: ba, ab, ba, ad
...
*/
while ( start >= 0 && end < len ) {
if ( start == end ) {
dp [ start ][ end ] = true ;
} else {
dp [ start ][ end ] = s . charAt ( start ) == s . charAt ( end ) && getDP ( dp , start + 1 , end - 1 );
}
if ( dp [ start ][ end ] && l >= max ) {
longest = s . substring ( start , end + 1 );
max = end - start + 1 ;
}
start ++ ;
end ++ ;
}
}
return longest ;
}
private boolean getDP ( boolean [][] dp , int start , int end ) {
if ( start <= end ) return dp [ start ][ end ] ;
return true ; // start > end 的時候,代表已超過邊界,會發生在偶數子字串且長度為 2 的情況 ex: (0,1) bb
}
}
這個解法的時間複雜度和前者相同為 O(n²):和暴力法同樣窮舉了所有子字串的組合,但節省了每次計算是否為回文的成本,改用記憶法代替。而空間複雜度的部分,由於需要組成一個 2D Array,同樣為 O(n²)。
下面影片都講解得很清楚~推!
VIDEO VIDEO